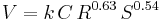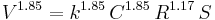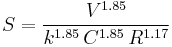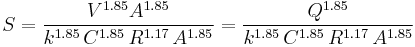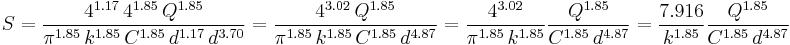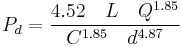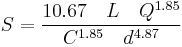Hazen–Williams equation

The Hazen–Williams equation is an empirical formula which relates the flow of water in a pipe with the physical properties of the pipe and the pressure drop caused by friction. It is used in the design of water pipe systems[1] such as fire sprinkler systems[2], water supply networks, and irrigation systems. It is named after Allen Hazen and Gardner Stewart Williams.

The Hazen–Williams equation has the advantage that the coefficient C is not a function of the Reynolds number, but it has the disadvantage that it is only valid for water. Also, it does not account for the temperature or viscosity of the water.[3]

Contents

General form

The general form of the equation relates the mean velocity of water in a pipe with the geometric properties of the pipe and slope of the energy line.

V = k\, C\, R^{0.63}\, S^{0.54}

where:

Typical C factors used in design, which take into account some increase in roughness as pipe ages are as follows:[4]

Material C Factor low C Factor high Reference
Asbestos-cement 140 140 -
Cast iron 100 140 -
Cement-Mortar Lined Ductile Iron Pipe 140 140 -
Concrete 100 140 -
Copper 130 140 -
Steel 90 110 -
Galvanized iron 120 120 -
Polyethylene 140 140 -
Polyvinyl chloride (PVC) 130 130 -
Fibre-reinforced plastic (FRP) 150 150 -

Pipe equation

The general form can be specialized for full pipe flows. Taking the general form

V = k\, C\, R^{0.63}\, S^{0.54}

and exponentiating each side by 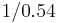1/0.54 gives (rounding exponents to 2 decimals)

V^{1.85} = k^{1.85}\, C^{1.85}\, R^{1.17}\, S

Rearranging gives

S = {V^{1.85} \over k^{1.85}\, C^{1.85}\, R^{1.17}}

The flow rate Q = V A, so

S = {V^{1.85} A^{1.85}\over k^{1.85}\, C^{1.85}\, R^{1.17}\, A^{1.85}} = {Q^{1.85}\over k^{1.85}\, C^{1.85}\, R^{1.17}\, A^{1.85}}

The hydraulic radius R (which is different from the geometric radius r) for a full pipe of geometric diameter d is d/4; the pipe's cross sectional area A is 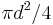\pi d^2 / 4, so

S = {4^{1.17}\, 4^{1.85}\,Q^{1.85}\over \pi^{1.85}\,k^{1.85}\, C^{1.85}\, d^{1.17}\, d^{3.70}} = {4^{3.02}\,Q^{1.85}\over \pi^{1.85}\,k^{1.85}\, C^{1.85}\, d^{4.87}} = { 4^{3.02} \over \pi^{1.85}\,k^{1.85}} {Q^{1.85}\over C^{1.85}\, d^{4.87}} = { 7.916 \over k^{1.85}} {Q^{1.85}\over C^{1.85}\, d^{4.87}}

U.S. customary units (Imperial)

When used to calculate the pressure drop using the US customary units system, the equation is:

P_d=\frac{4.52\quad L\quad Q^{1.85}}{C^{1.85}\quad d^{4.87}}

where:

Pd = pressure drop over a length of pipe, psig (pounds per square inch gauge pressure)

L = length of pipe, ft (feet)

Q = flow, gpm (gallons per minute)

d = inside pipe diameter, in (inchs)

SI units

When used to calculate the pressure drop with the International System of Units, the equation becomes:[5]

S = \frac{10.67\quad L \quad Q^{1.85}}{C^{1.85}\quad d^{4.87}}

where:

See also

References

Notes

  1. ^ "Hazen–Williams Formula". http://docs.bentley.com/en/HMFlowMaster/FlowMasterHelp-06-05.html. Retrieved 2008-12-06. 
  2. ^ "Hazen–Williams equation in fire protection systems". Canute LLP. 27 January 2009. http://www.canutesoft.com/index.php/Basic-Hydraulics-for-fire-protection-engineers/Hazen-Williams-formula-for-use-in-fire-sprinkler-systems.html. Retrieved 2009-01-27. 
  3. ^ Brater, Errest; King Horace (1996). "6". Handbook of Hydraulics. Lindell E. James (Seventh Edition ed.). New York: Mc Graw Hill. pp. 6.29. ISBN 0-07-007247-7. 
  4. ^ Engineering toolbox Hazen–Williams coefficients
  5. ^ "Comparison of Pipe Flow Equations and Head Losses in Fittings" (PDF). http://rpitt.eng.ua.edu/Class/Water%20Resources%20Engineering/M3e%20Comparison%20of%20methods.pdf. Retrieved 2008-12-06. 

External links